The concept of Byzantine Fault Tolerance (BFT) has many implications for modern technologies like blockchain. In distributed systems, achieving consensus among multiple nodes is a critical challenge. But what happens when some of these nodes are not just failing, but actively misbehaving?
The Byzantine Generals Problem
The concept of Byzantine failures is rooted in the Byzantine Generals Problem, introduced in a 1982 paper by Leslie Lamport, Robert Shostak, and Marshall Pease. Imagine several generals, each with their own army, trying to coordinate an attack on a city. They can only communicate via messengers, and worse yet, some generals or messengers might be traitors, sending conflicting information to different recipients.
This scenario illustrates the core challenge of Byzantine fault tolerance: how can we reach consensus when some participants in the system might be actively working against us?
Practical Byzantine Fault Tolerance (PBFT)
In 1999, Miguel Castro and Barbara Liskov proposed the Practical Byzantine Fault Tolerance (PBFT) algorithm, a landmark development in the field. PBFT was the first solution capable of handling Byzantine failures while maintaining high performance in real-world systems.
Key features of PBFT include:
- Use of cryptographic methods to authenticate communication and prevent tampering.
- Requirement of at least 3f + 1 total nodes to tolerate f faulty nodes.
- A three-phase protocol (pre-prepare, prepare, and commit) to ensure consensus.
PBFT allows a system to tolerate up to one-third of its nodes being faulty or malicious, a significant improvement over previous algorithms.
From PBFT to Blockchain
While PBFT was groundbreaking, it had limitations, particularly in terms of scalability. Enter blockchain technology, which combines ideas from Byzantine consensus with other concepts:
- Proof of Work: Participants (miners) must solve cryptographic puzzles to add entries to the chain, making it computationally expensive to misbehave.
- Incentive Structures: Good behavior is rewarded with cryptocurrencies, encouraging participants to act honestly.
These innovations allow blockchain systems to achieve consensus probabilistically, with lower requirements for the number of nodes needed to reach agreement.
The Ongoing Evolution of BFT
The rise of blockchain has sparked renewed interest in Byzantine fault tolerance. Researchers continue to explore new algorithms and approaches, balancing factors like performance, trust assumptions, and decentralization.
As distributed systems become increasingly central to our digital infrastructure, understanding and improving Byzantine fault tolerance remains a crucial area of study. Whether developing the next breakthrough in blockchain technology or simply trying to coordinate lunch plans with unreliable colleagues, the principles of BFT offer valuable insights into achieving consensus in an imperfect world.
Key Concepts
Byzantine Fault Tolerance (BFT) The ability of a distributed system to continue functioning correctly even when some of its components fail or actively misbehave (act maliciously or arbitrarily incorrectly).
Byzantine Failure A type of failure in a distributed system where a component continues to operate but sends incorrect or inconsistent information, either due to malicious intent or arbitrary faults.
Byzantine Generals Problem A thought experiment illustrating the challenges of reaching consensus in a distributed system with potentially unreliable or malicious participants.
Consensus Agreement among participants in a distributed system on a single data value or state, even in the presence of failures or malicious behavior.
Distributed System A network of independent computers that appear to users as a single coherent system, working together to accomplish a common goal.
Practical Byzantine Fault Tolerance (PBFT) An algorithm proposed by Castro and Liskov in 1999 that efficiently solves the Byzantine Generals Problem for asynchronous systems, tolerating up to one-third Byzantine faults.
Blockchain A distributed ledger technology that maintains a growing list of records (blocks) that are cryptographically linked and secured against tampering and revision.
Distributed Ledger A consensually shared and synchronized digital database spread across multiple sites, institutions, or geographies.
Proof of Work A system that requires a not-insignificant but feasible amount of effort to deter frivolous or malicious uses of computing power, such as sending spam emails or launching denial of service attacks.
Miner In blockchain systems, a participant who validates new transactions and records them on the blockchain.
Cryptographic Puzzle A mathematical problem that is difficult to solve but easy to verify, often used in proof-of-work systems.
Incentive Structure A system of rewards and penalties designed to encourage desired behaviors and discourage undesired ones within a network or organization.
Permissionless vs. Permissioned Systems
- Permissionless: Systems where anyone can participate without needing approval (e.g., Bitcoin).
- Permissioned: Systems where participants must be approved or invited to join (e.g., some enterprise blockchain solutions).
Asynchronous Communication A mode of communication in distributed systems where there is no fixed upper bound on message delivery times.
Quorum The minimum number of votes that a distributed transaction has to obtain in order to be allowed to perform an operation in a distributed system.
Review Questions
Describe the Byzantine Generals problem?
The Byzantine Generals problem, introduced by Leslie Lamport, Robert Shostak, and Marshall Pease in 1982, is a thought experiment that illustrates the challenges of achieving consensus in distributed systems when faced with potentially malicious or arbitrary failures.
In this problem, multiple generals with their armies are positioned around a city they want to attack. They need to decide together whether to attack or retreat, as a coordinated action is required for success. However, they can only communicate through messengers who must travel through mountains. Some generals or messengers might be traitors (Byzantine failures) who send conflicting or incorrect messages to different recipients. The challenge is how to ensure all loyal generals can reach consensus on a coordinated plan despite these Byzantine failures that could corrupt messages or provide inconsistent information to different generals.
Why can you not solve the Byzantine Generals problem with a consensus algorithm like Paxos?
You cannot solve the Byzantine Generals problem with a consensus algorithm like Paxos because Paxos was designed to handle only benign failures (fail-stop failures), not Byzantine failures. In benign failures, nodes simply crash or stop responding, but they do not behave maliciously.
Byzantine failures are more complex because faulty nodes continue participating in the distributed system but exhibit incorrect behavior - they may send contradictory messages to different participants or otherwise attempt to sabotage the system. Paxos assumes that nodes either work correctly or fail completely, not that they might deliberately lie or send inconsistent messages, which is the core challenge in Byzantine failures.
This is why Byzantine Fault Tolerance requires more complex protocols like pBFT (Practical Byzantine Fault Tolerance) and requires more replicas (3f+1 versus 2f+1 for Paxos) to tolerate f failures.
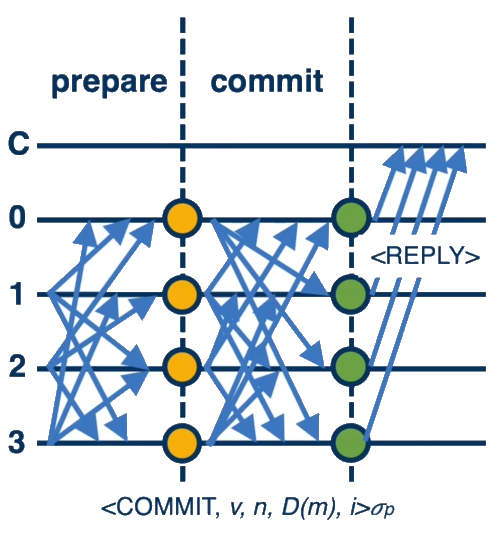
Describe the pBFT algorithm? What is the goal of each of the phases in the algorithm?
The Practical Byzantine Fault Tolerance (pBFT) algorithm, developed by Miguel Castro and Barbara Liskov in 1999, allows a distributed system to reach consensus despite Byzantine failures. The algorithm operates in a view-based system with a primary replica and backup replicas, requiring 3f+1 total replicas to tolerate f faulty replicas.
The pBFT protocol involves three main phases:
-
Pre-prepare phase:
- Goal: The primary assigns a sequence number to a client request and proposes this ordering to all backups.
- Process: The primary multicasts a "pre-prepare" message with the client's request, a view number, and sequence number.
- Backups verify the message authenticity, view correctness, and that the sequence number is within appropriate watermarks before accepting.
-
Prepare phase:
- Goal: Ensure all non-faulty replicas agree on the same order for requests within a view, even if the primary is faulty.
- Process: If a backup accepts the pre-prepare message, it enters the prepare phase by multicasting a "prepare" message to all other replicas.
- Each replica waits for 2f matching prepare messages from different replicas (along with the pre-prepare) to ensure the predicate "prepared(m,v,n,i)" becomes true.
-
Commit phase:
- Goal: Ensure agreement on request ordering across different views, guaranteeing that committed requests remain committed even during view changes.
- Process: Once the prepare phase completes, a replica multicasts a "commit" message to all replicas.
- A replica waits for 2f+1 matching commit messages (including its own) to satisfy the "committed-local" predicate before executing the request and sending a reply to the client.
The client waits for f+1 identical replies from different replicas to accept a result, ensuring that at least one non-faulty replica produced that result.
Why does Paxos need 2f+1 nodes to tolerate f failures, and pBFT needs 3f+1?
Paxos needs 2f+1 nodes to tolerate f failures because it only handles benign failures (fail-stop). With 2f+1 total nodes, even if f nodes fail, the remaining f+1 nodes (a majority) can still reach consensus.
pBFT needs 3f+1 nodes to tolerate f Byzantine failures for these mathematical reasons:
-
When making decisions, the system must be able to proceed after communicating with n-f nodes (since f might be non-responsive).
-
Among these n-f nodes that respond, up to f might be Byzantine/faulty and sending incorrect information.
-
To ensure that non-faulty responses outnumber potentially faulty ones among the responders, we need: (n-f) - f > f
-
Solving this inequality: n - 2f > f, which gives us n > 3f, or n ≥ 3f+1
This means with 3f+1 total nodes, even if f nodes are Byzantine faulty and trying to subvert the system, the protocol can still reach consensus because the n-f nodes that participate will contain at least f+1 honest nodes that outweigh the f faulty ones.
Relate on a high-level a blockchain distributed ledger and a Paxos log
At a high level, both a blockchain distributed ledger and a Paxos log aim to maintain consistent, ordered records across distributed systems, but they have key differences in their design and fault tolerance:
Similarities:
- Both maintain an ordered sequence of records (transactions or state changes)
- Both ensure consistency across distributed participants
- Both aim to have participants agree on the sequence of records
Differences:
- Fault Tolerance Model: Blockchain technologies typically handle Byzantine failures (malicious participants), while Paxos handles only benign failures.
- Structure: A blockchain is explicitly designed as a chain of blocks linked by cryptographic hashes, while Paxos maintains a log of commands.
- Participation: Blockchains often operate in permissionless environments where anyone can join, while Paxos typically runs in closed, permissioned systems with known participants.
- Approach to Consensus: Bitcoin-style blockchains often use proof-of-work to establish consensus probabilistically, while Paxos relies on majority votes from a known set of participants.
- Finality: Paxos provides immediate finality once consensus is reached, while blockchain systems often have probabilistic finality that strengthens over time.
Why is Paxos or Raft consensus not used in practice in Blockchain technologies?
Paxos or Raft consensus algorithms are not commonly used in public blockchain technologies for several reasons:
-
Byzantine Fault Model: Paxos and Raft only handle benign failures, not Byzantine failures where participants might behave maliciously. Public blockchains need to operate in adversarial environments where some participants may actively try to subvert the system.
-
Known Participation: Paxos and Raft assume a known set of participants, while public blockchains often operate in permissionless environments where anyone can join or leave.
-
Scalability Limitations: The communication complexity of Paxos is high (O(n²) or worse), making it impractical for large-scale blockchain networks with potentially thousands of participants.
-
Fixed Number of Failures: Paxos requires knowing the maximum number of failures (f) in advance and configuring the system with n > 2f nodes. In public blockchains, the number of potential attackers is not known in advance.
-
Identity Verification: Traditional consensus protocols assume verified identities, while public blockchains often operate in pseudonymous environments where creating multiple identities (Sybil attacks) is possible.
Instead, blockchain technologies use alternative approaches like Proof-of-Work, Proof-of-Stake, or hybrid solutions that combine Byzantine fault tolerance with economic incentives and cryptographic techniques.
What is the role of the PoW and cryptocurrency incentives used in Blockchain consensus solutions?
The roles of Proof-of-Work (PoW) and cryptocurrency incentives in blockchain consensus solutions are:
-
Sybil Attack Prevention: PoW makes it computationally expensive to participate in consensus, preventing attackers from creating multiple identities to gain majority control (Sybil attacks).
-
Participation Control: Unlike traditional Byzantine fault tolerance protocols that require exactly 3f+1 known participants, PoW allows anyone to participate but makes participation costly, effectively controlling who can meaningfully contribute to consensus.
-
Economic Security: Cryptocurrency incentives create an economic security model where honest behavior is financially rewarded, while attacks become prohibitively expensive.
-
Decentralization Enablement: The combination of PoW and incentives allows blockchain systems to operate without central authorities or pre-established trust, as the protocol itself establishes trust through cryptographic proofs and economic incentives.
-
Probabilistic Finality: PoW provides probabilistic finality that strengthens over time as more blocks are added, allowing the system to continue operating even when network conditions are unpredictable.
-
Self-Regulation: Economic incentives create a self-regulating system where participants are motivated to follow the protocol rules to maximize their rewards, reducing the need for external enforcement.
These mechanisms together allow blockchain systems to achieve consensus in permissionless environments where the number and identity of participants are unknown and potentially malicious.
What is James Mickens' Saddest Moment?
James Mickens' "Saddest Moment" refers to a humorous article he wrote in USENIX about his experience with Byzantine fault tolerance papers. In this piece, he comically laments the complexity and impenetrability of papers on Byzantine fault tolerance, joking about the difficulty that computer scientists outside the field of theoretical distributed computing have in understanding the nuanced differences among Byzantine fault tolerance algorithms.
The title "The Saddest Moment" refers to his exaggerated despair when confronted with the complex diagrams and theoretical discussions in these papers. Mickens humorously illustrates this with a typical diagram from a Byzantine fault paper showing a complex network protocol. He also jokes about the broad applicability of these protocols, suggesting how they might be used for mundane tasks like making lunch plans with colleagues.
The article is known for its comedic take on the sometimes overwhelming complexity of distributed systems research, particularly Byzantine fault tolerance.