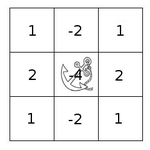
Some libraries produce image convolutions assuming the kernel is rotated 180 degrees - OpenCV does not. This post will quickly show that OpenCV does not rotate the image using a quick C++ implementation.
First, let's take a look at MATLAB's documentation on convolutions...
Convolution
Linear filtering of an image is accomplished through an operation called convolution. Convolution is a neighborhood operation in which each output pixel is the weighted sum of neighboring input pixels. The matrix of weights is called the convolution kernel, also known as the filter. A convolution kernel is a correlation kernel that has been rotated 180 degrees.
For example, suppose the image is
A = [17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9]
and the convolution kernel is
h = [8 1 6
3 5 7
4 9 2]
The following figure shows how to compute the (2,4) output pixel using these steps:
- Rotate the convolution kernel 180 degrees about its center element.
- Slide the center element of the convolution kernel so that it lies on top of the (2,4) element of A.
- Multiply each weight in the rotated convolution kernel by the pixel of A underneath.
- Sum the individual products from step 3.
So let's try this in OpenCV using C++...
#include <opencv2/opencv.hpp>
#include <iostream>
/// <summary>
/// Prints the matrix.
/// </summary>
/// <param name="mat">The matrix (pointer).</param>
void printMat(cv::Mat* mat)
{
printf("(%dx%d)\n", mat->cols, mat->rows);
for (int i = 0; i < mat->rows; i++)
{
if (i == 0)
{
for (int j = 0; j < mat->cols; j++) printf("%10d", j + 1);
}
printf("\n%4d: ", i + 1);
for (int j = 0; j < mat->cols; j++)
{
printf("%10.2f", mat->at<float>(i, j));
}
}
printf("\n");
}
/// <summary>
/// The main function
/// </summary>
/// <param name="argc">The argument count.</param>
/// <param name="argv">The argument vector.</param>
/// <returns>0 for success</returns>
int main(int argc, char** argv)
{
// Create the original matrix
// CV_32FC1 means "32 bit float, 1 channel"
// Note: sizeof(float) = 4 and 4*8 = 32
cv::Mat original = cv::Mat(3, 3, CV_32FC1);
// Create the kernel
cv::Mat filter = cv::Mat(3, 3, CV_32FC1);
// Set everything to 0
for (int r = 0; r < 3; r++) {
for (int c = 0; c < 3; c++) {
original.at<float>(r, c) = 0.0;
filter.at<float>(r, c) = 0.0;
}
}
// Specify the bottom right = 1.0 for testing
original.at<float>(2, 2) = 1.0;
filter.at<float>(2, 2) = 1.0;
cv::Mat filtered;
// Convolve a matrix with the kernel
filter2D(original, filtered,
-1, // -1 for same as source
filter, // the filter just specified
cv::Point(-1, -1), // cv::Point(-1, -1) is the center
0, // value added to each pixel
cv::BORDER_ISOLATED // do not look outside of ROI
);
printf("Starting matrix:\n");
printMat(&original);
printf("\nFilter matrix:\n");
printMat(&filter);
printf("\nFiltered matrix:\n");
printMat(&filtered);
return 0;
}
Here's the results:
Starting matrix:
(3x3)
1 2 3
1: 0.00 0.00 0.00
2: 0.00 0.00 0.00
3: 0.00 0.00 1.00
Filter matrix:
(3x3)
1 2 3
1: 0.00 0.00 0.00
2: 0.00 0.00 0.00
3: 0.00 0.00 1.00
Filtered matrix:
(3x3)
1 2 3
1: 0.00 0.00 0.00
2: 0.00 1.00 0.00
3: 0.00 0.00 0.00
What does this mean? This implies the calculation for the middle element is
1 2 3
1: 0.00 0.00 0.00
2: 0.00 0.00 0.00
3: 0.00 0.00 1.00 * 1.00
Given that the image matrix is
1 2 3
1: 0.00 0.00 0.00
2: 0.00 0.00 0.00
3: 0.00 0.00 1.00
and the filter matrix is
1 2 3
1: 0.00 0.00 0.00
2: 0.00 0.00 0.00
3: 0.00 0.00 1.00
It it should be clear that OpenCV does not rotate the convolution kernel.
If so, the calculation would look like
1 2 3
1: 0.00* 1.00 0.00 0.00
2: 0.00 0.00 0.00
3: 0.00 0.00 1.00 * 0.00
Which would produce a matrix of all zeros.